BB - Suponha que para a divulgação de produtos oferecidos pelo Banco do Brasil no primeiro trimestre deste ano, 1.295 folhetos foram entregues aos clientes em janeiro e que o total entregue nos dois meses seguintes foi o dobro desse valor. Se o numero de folhetos entregues em março ultrapassou o de fevereiro em 572 unidades, a soma dos números de folhetos entregues em janeiro e fevereiro foi?
J= 1.295
F + M = 2X(1925)
M= F+572 => J + F ?
F + M = 2590
F + F + 572 = 2590
2F = 2590 – 572 = 2018 QUE SERÁ DIVIDO POR 2 ENTÃO F = 1009. F = 1295 + 1009 = 2.304.
terça-feira, 31 de maio de 2011
segunda-feira, 30 de maio de 2011
Prova do Banco do Brasil - 2010
Prova do Banco do Brasil - 2010 - FCC) Pesquisadores descobriram que o uso do fundo preto nas páginas de busca da internet produz um consumo menor de energia em relação à tela branca. Se todas as buscas fossem feitas com tela preta, a economia total em um tempo médio de 10 segundos seria equivalente à energia gasta por 77 milhões de geladeiras ligadas ininterruptamente durante 1 hora. Nessas condições, a economia total em um tempo médio de buscas de 30 minutos seria equivalente à energia gasta por essas geladeiras ligadas ininterruptamente durante
(A) 8 dias.
(B) 7 dias e meio.
(C) 5 dias.
(D) 3 dias.
(E) 2 dias e meio.
SOLUÇÃO
Temos uma regra de três simples:
Seg Tempo
10 seg 1h
1800 seg x
x=1800/10=180 horas =7,5 dias
Resposta: B
(A) 8 dias.
(B) 7 dias e meio.
(C) 5 dias.
(D) 3 dias.
(E) 2 dias e meio.
SOLUÇÃO
Temos uma regra de três simples:
Seg Tempo
10 seg 1h
1800 seg x
x=1800/10=180 horas =7,5 dias
Resposta: B
sexta-feira, 27 de maio de 2011
Regras de conversão de unidades de medida
Quilômetro km | Hectômetro hm | Decâmetro dam | Metro m | Decímetro dm | Centímetro cm | Milímetro mm |
1000 m | 100 m | 10 m | 1 m | 0,1 m | 0,01 m | 0,001 m |
Regras Práticas:
- Para passar de uma unidade para outra imediatamente inferior devemos fazer uma multiplicação por 10.
Ex : 1 m = 10 dm
- Para passar de uma unidade para outra imediatamente superior, devemos fazer uma divisão por 10.
- Para passar de uma unidade para outra qualquer, basta aplicar sucessivas vezes uma das regras anteriores.
1 m = 0,001 km
Quilômetro quadrado km2 | Hectômetro quadrado hm2 | Decâmetro quadrado dam2 | Metro quadrado m2 | Decímetro quadrado dm2 | Centímetro quadrado cm2 | Milímetro quadrado mm2 |
1x106 m2 | 1x104 m2 | 1x102 m2 | 1 m2 | 1x10-2 m2 | 1x10-4 m2 | 1x10-6 m2 |
Regras Práticas:
- Para passar de uma unidade para outra imediatamente inferior devemos fazer uma multiplicação por 100.
- Para passar de uma unidade para outra imediatamente superior, devmos fazer uma divisão por 100.
- Para passar de uma unidade para outra qualquer, basta aplicar sucessivas vezes uma das regras anteriores.
Quilômetro cúbico km3 | Hectômetro cúbico hm3 | Decâmetro cúbico dam3 | Metro cúbico m3 | Decímetro cúbico dm3 | Centímetro cúbico cm3 | Milímetro cúbico mm3 |
1x109 m3 | 1x106 m3 | 1x103 m3 | 1 m3 | 1x10-3 m3 | 1x10-6 m3 | 1x10-9 m3 |
Regras Práticas:
- Para passar de uma unidade para outra imediatamente inferior devemos fazer uma multiplicação por 1000.
- Para passar de uma unidade para outra imediatamente superior, devemos fazer uma divisão por 1000.
- Para passar de uma unidade para outra qualquer, basta aplicar sucessivas vezes uma das regras anteriores.
O litro( l ) é uma medida de volume muito comum e que corresponde a 1 dm3.
1 litro = 0,001 m3 => 1 m3 = 1000 litros
1 litro = 1 dm3
1 litro = 1.000 cm3
1 litro = 1.000.000 mm3
Prefixos Usados no SI | ||
Prefixos | Símbolos | Fator de multiplicação da unidade |
Tera | T | 1012 |
Giga | G | 109 |
Mega | M | 106 |
Quilo | k | 103 |
Hecto | h | 102 |
Deca | da | 101 |
Deci | d | 10-1 |
Centi | c | 10-2 |
Mili | m | 10-3 |
Micro | m | 10-6 |
Nano | n | 10-9 |
Pico | p | 10-12 |
Fento | f | 10-15 |
Atto | a | 10-18 |
quarta-feira, 25 de maio de 2011
Permutação
Considere o conjunto {1,2,3,4,5}. Quantos subconjuntos de 3 elementos se pode fazer?
5!/3!= 5.4.3.2.1/3.2.1=20
5!/3!= 5.4.3.2.1/3.2.1=20
terça-feira, 24 de maio de 2011
-Numa cidade,os números de telefone são formados de um prefixo de quatro algarismos , seguidos de outros quatro algarismos. Quantos números de telefone existem com o prefixo 6421?
6421-0000
6421-0001...
...6421-9999
São 9999 numeros diferente + 1 por que que tem o ''0000'' seriam então 10000 números de telefone
-Um sindicato pretende realizar eleições para ocupar os cargos de presidente, vice-presidente e secretário. Sabendo que há 8 pessoas igualmente qualificadas, de quantas maneiras podemos formar essa chapa? (não pode haver acumulo de cargos)
8!/(8-3)! = 8.7.6.5.4.3.2.1/5.4.3.2.1=336
6421-0000
6421-0001...
...6421-9999
São 9999 numeros diferente + 1 por que que tem o ''0000'' seriam então 10000 números de telefone
-Um sindicato pretende realizar eleições para ocupar os cargos de presidente, vice-presidente e secretário. Sabendo que há 8 pessoas igualmente qualificadas, de quantas maneiras podemos formar essa chapa? (não pode haver acumulo de cargos)
8!/(8-3)! = 8.7.6.5.4.3.2.1/5.4.3.2.1=336
segunda-feira, 23 de maio de 2011
Arranjo
Quantas placas de automóveis com três letras e quatro números podemos formar, dispondo de 26 letras e 10 algarismos?
a)60.000
b)153.000
c)80.000
d)175.760.000
26^3 = 17576
10^4=1000
17576 . 1000 = 175.760.000
letra d
a)60.000
b)153.000
c)80.000
d)175.760.000
26^3 = 17576
10^4=1000
17576 . 1000 = 175.760.000
letra d
sexta-feira, 20 de maio de 2011
Arranjo
Com os algarismos 1,2,3,4, sem repeti-los, podemos escrever 'x' números maiores que 2.400. O valor de "X' é?
Primeiro: usando os algarismos 1,2,3 e 4, sem repeti-los p/formar um número maior do que 2400, então o algarismo que irá representar a primeira casa não pode ser 1, pois qualquer número de quatro algarismos que comece com 1 é menor do que 2400.
Usando o 2 como primeiro algarismo:
2_ _ _
Para esse número ser maior do que 2400 e utilizando somente os algarismos 1,3 e 4, só se a segunda casa for ocupada pelo algarismo 4:
2 4_ _
Então, a terceira casa pode ser ocupada por dois outros algarismos e a quarta casa pelo algarismo que restou.
Com cálculos:
2x1=2
Usando o 3 como primeiro algarismo:
3_ _ _
Qualquer número de quatro algarismo começado por 3 é maior do que 2400. Na segunda casa podemos usar 3 outros algarismos, na terceira casa podemos usar dois outros algarismos e na última usa-se o que restou. Traduzindo o que eu escrevi em cálculo:
3x2x1=6
Usando o 4 como primeiro algarismo:
4_ _ _
Qualquer número de quatro algarismo começado por 4 é maior do que 2400. Na segunda casa podemos usar 3 outros algarismos, na terceira casa podemos usar dois outros algarismos e na última usa-se o que restou. Traduzindo o que eu escrevi em cálculo:
3x2x1=6
Somando as possibilidades:
2+6+6=14
Usando o 2 como primeiro algarismo:
2_ _ _
Para esse número ser maior do que 2400 e utilizando somente os algarismos 1,3 e 4, só se a segunda casa for ocupada pelo algarismo 4:
2 4_ _
Então, a terceira casa pode ser ocupada por dois outros algarismos e a quarta casa pelo algarismo que restou.
Com cálculos:
2x1=2
Usando o 3 como primeiro algarismo:
3_ _ _
Qualquer número de quatro algarismo começado por 3 é maior do que 2400. Na segunda casa podemos usar 3 outros algarismos, na terceira casa podemos usar dois outros algarismos e na última usa-se o que restou. Traduzindo o que eu escrevi em cálculo:
3x2x1=6
Usando o 4 como primeiro algarismo:
4_ _ _
Qualquer número de quatro algarismo começado por 4 é maior do que 2400. Na segunda casa podemos usar 3 outros algarismos, na terceira casa podemos usar dois outros algarismos e na última usa-se o que restou. Traduzindo o que eu escrevi em cálculo:
3x2x1=6
Somando as possibilidades:
2+6+6=14
Arranjo
Um sindicato pretende realizar eleiçoes para ocupar os cargos de presidente, vice-presidente e secretario. Sabendo q ha 8 pessoas igualmente qualificadas, de quantas maneiras podemos formar esta chapa? (nao pode haver acumulo de cargos).
8 * 7 * 6 = 336
quinta-feira, 19 de maio de 2011
segunda-feira, 16 de maio de 2011
domingo, 15 de maio de 2011
Números Reais
O conjunto dos números reais 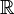 é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
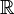 é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.Os números reais são números usados para representar uma quantidade contínua (incluindo o zero e os negativos). Pode-se pensar num número real como uma fracção decimal possivelmente infinita, como 3,141592(...). Os números reais têm uma correspondência biunívoca com os pontos de uma reta.
Denomina-se corpo dos números reais a colecção dos elementos pertencentes à conclusão dos racionais, formado pelo corpo de fracções associado aos inteiros (números racionais) e a norma associada ao infinito.
Existem também outras conclusões dos racionais, uma para cada número primo p, chamadas números p-ádicos. O corpo dos números p-ádicos é formado pelos racionais e a norma associada a p!
Assinar:
Comentários (Atom)
